AN EXPERIMENTAL DISPROOF OF
SPECIAL RELATIVITY THEORY
(Unipolar Induction)
by Francisco J. Müller
............
Here is an experiment that invalidates
Relativistic Electrodynamics. To facilitate understanding it will be presented
in two parts, each one in turn subdivided into a rotational case and a
translational one.
Part 1: SCHEMATIC RESULTS
A)Rotational Case
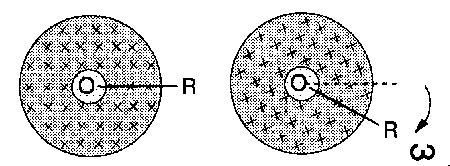FIGURE 1
|
|
A radial conductor OR rotates TOGETHER with a cylindrical
(or ring) magnet with speed omega. The B field enters the paper,
as indicated by the X's (Fig. 1) |
- - - In spite of the absence of relative
motion between magnet and wire a potential difference is induced between
0
and R due to the ABSOLUTE ROTATION of the system (Ref. 1). This
contradicts Einstein's statement at the beginning of his 1905 paper. It
does not violate Special Relativity, however, since this theory is not
applicable to rotating systems.
- - - Relativists like Schiff resort
to the General Theory, and attribute the induced voltage to the counter-rotation
of the distant Galaxies of the Universe which warp space/time (Ref. 2).
We do not believe in such a mystified warping. We reason as follows:
|
B)Translational Case
|
|
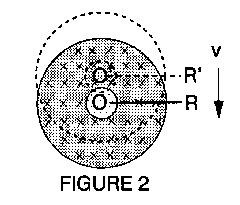
If instead of rotating the system we move it with linear
speed V (Fig.2), then there is NO INDUCTION along OR. Why?
The B field is the same; the speeds also are similar, and no
relative motion exists as in Figure 1. Why the difference? |
It seems that the Galaxies have a very
"fine eye", distinguishing a minute angular oscillation from a minute linear
translation, at light years away... and instantly! This sounds like science
fiction. Let us go BACK TO REALITY.
IN FIGURE 1 ALL THE VELOCITIES ARE PARALLEL, THAT IS, TANGENTIAL TO THE
MAGNETIC EDGES
|
|
IN FIGURE 2 MOST OF THE VELOCITIES HAVE COMPONENTS PERPENDICULAR TO THOSE
EDGES.
|
|
AS A RESULT, IN FIGURE 2 THE EDGES
PRODUCE MAGNETIC "STORMS" BY MOTION IN SPACE, (an absolute effect), WHICH
ARE EQUIVALENT TO NEGATIVE (VxB) EFFECTS. THE LATTER CANCEL THE
POSITIVE (VxB) FIELDS THUS YIELDING ZERO NET INDUCTION.
(All this can be proven using vector
algebra)
* * * P r e d i c t i o n * * *
An experiment could be designed that,
avoiding all transversal edges, might show induction without relative motion
between the local magnet and the wire, EVEN IN THE CASE OF RECTILINEAR
(INERTIAL) MOTION.
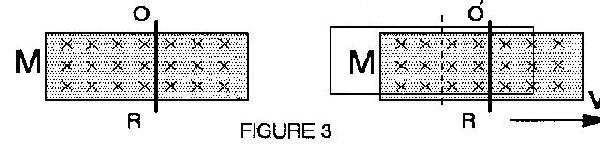
Consider the rectangular magnet M
of Fig. 3, (magnetized perpendicularly to the paper), and the transversal
conductor OR. If both move with linear velocity V as indicated
by the arrow, NO INDUCTION occurs along OR. This is in agreement
with the equations of Relativistic Electrodynamics. If V is accelerated,
still NO INDUCTION results. (Speed change is irrelevant)
Meaningless as it might appear consider
now the experiment of Fig. 4:
|
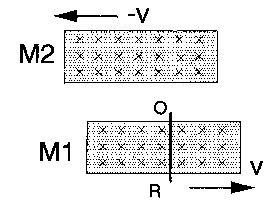
FIGURE 4
|
|
This is as in Fig. 3, but with an additional magnet M2 moving
in the opposite direction.
--Again, practically NO INDUCTION occurs along OR, especially
if the return fields of the magnets do not touch" each other.
NOW COMES THE CRUCIAL STEP:
|
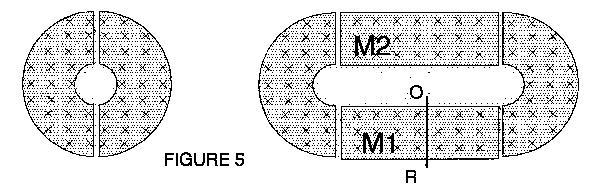
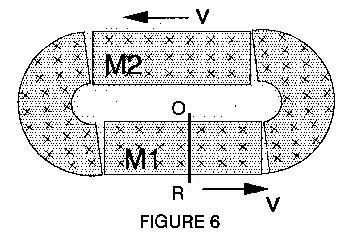
Take a ring magnet similar to the one
in Figure 1 and cut it in halves, (Fig. 5). Separate them and insert the
rectangular magnets M2 and Ml with conductor OR fixed
to the latter.
In this way all
transversal edges are avoided, making a continuous magnetic system. If
small gaps are left as shown in Fig. 5 then Ml and M2 can
be slightly displaced as shown in Fig. 6. Then AN INDUCTION OCCURS ALONG
OR!!!
|
BUT SPECIAL RELATIVITY PREDICTS NO INDUCTION just as in Figure
4. Hence, the Theory FAILS! And General Relativity cannot come to the rescue."
Both fail to account for the edge effect "at a distance".
|
|
Part II: EXPERIMENTAL DETAILS
Perhaps the reader is wondering if I made
all the experiments described in Part I. How can one measure a voltage
in an isolated piece of wire? In principle this is possible, by inserting
electrometers at the midpoint of the wire. But it is very difficult. What
I did was to use complete circuits in which all sections, except OR,
were shielded from the magnetic field. For this purpose I modified Faraday's
debated "unipolar inductor' of 1832. In what follows I will describe this
modification, basic for all my experiments.
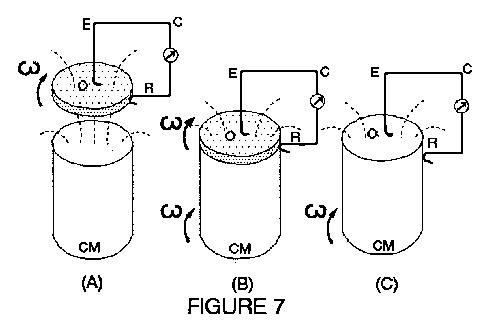
Faraday's Unipolar Inductor
A) Rotational Case
|
|
Rotating a copper disk above a magnet (Fig. 7A) Faraday
induced a current in OECR. Rotating disk AND magnet together he
obtained the same result, (Fig. 7B) and also removing the disk altogether
(Fig. 7C). WHERE is the seat of induction in the latter case? Along OR,
within the magnet? Or along ECR? |
To answer this hotly debated question
consider the following modification:
Müller's modification to the Unipolar
Inductor
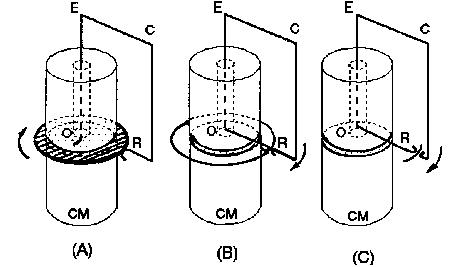
FIGURE 8
|
|
- - - Fig. 8 shows how the disk was set between two magnets;
then substituted by a collector ring and finally eliminated to have a complete
filamentary circuit, OECR. At R a sliding contact allowed
rotating OR or CR independently of each other. The cylindrical
magnet CM can also rotate about its axis, OE. |
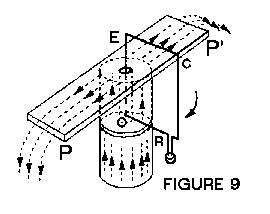
| Next, an iron plate PP' was inserted as shown in
Fig. 9 so that ECR is shielded from the magnetic lines. Only OR
"touches" the lines in the gap between the magnets. A mercury cup can substitute
for the sliding contact at R. |
|
 |
|
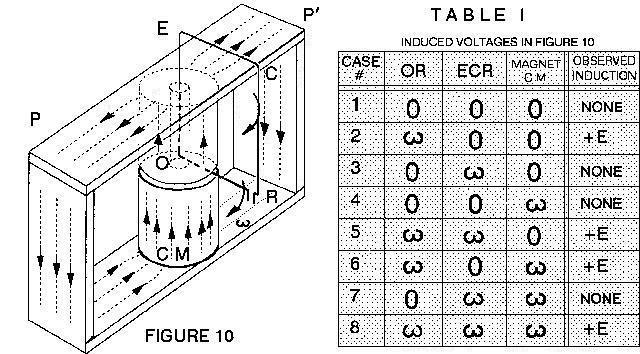
Finally, more plates were added to confine the return magnetic field within
a rectangular yoke, as shown in Fig. 10. (Rotations were limited to small
angles).
|
With this system 8 cases of relative motion can be studied as indicated
in TABLE 1, where omega means rotation and 0 means rest.
A voltage +E or -E was induced in cases 2, 5, 6 and 8, that
is, only when OR moved, regardless of its motion relative to the
cylindrical magnet CM. (The yoke PP' never moved). In cases
6 and 8, there was no relative motion between OR and CM.
Yet, a positive E occurred. The reciprocal cases, 3 and 1 respectively,
both gave zero E, violating the expected relativistic equivalence
of relative motions. In particular, case 8 is totally unexplainable by
the Lorentz transformation of the fields. Serious relativists like Panofsky
and Phillips (Ref. 1) accept that Special Relativity fails in this case,
and refer to Schiff (Ref. 2) who in turn uses General Relativity and brings
the "galaxies" into the problem. But this is unbelievable and useless as
explained in PART 1. The rectilinear variation of Faraday's inductor proves
the point. Practical details follow.
B) The Translational Case:
Müller's Linear Unipolar Inductor
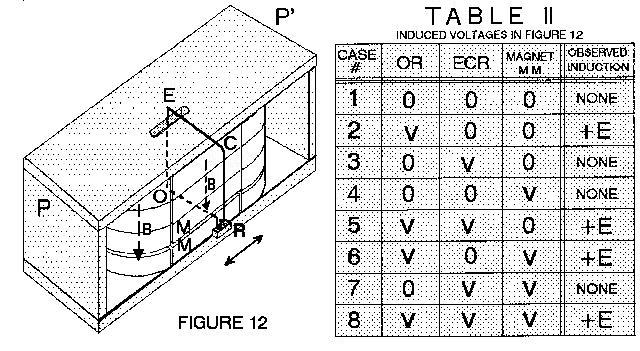
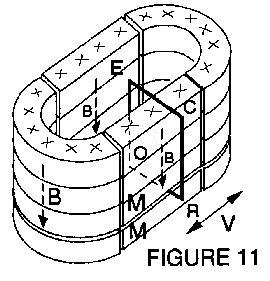
The "racetrack" magnets of Figs. 5 and 6 were piled up forming four
layers as shown in Fig. 11. A gap between the two lower layers allowed
inserting the insulated rectangular loop OECR. A mercury cup at
R
(not shown) allows independent rectilinear motion of OR,
ECR
and magnets M as indicated by the double arrow V. |
 |
Finally, add plates PP' to confine the magnetic field totally within
an iron yoke, as shown in Fig. 12. (Motions are limited to small linear
displacements).
- - The induction results, for the various cases of relative motion, are
given in TABLE II. The reader can note that these are identical to the
results of TABLE I except that the motions are now inertial instead of
rotational. In particular we note cases 6 and 8, in which the wire OR
comoves with the magnets MM and yet, THERE IS A POSITIVE INDUCTION
+E.
This induction is located at OR and not at ECR, since the
latter lies in a field free region and its motion is irrelevant. (ECR
moves in case 8 but not in case 6; yet, both cases yield +E).
BRIEF DISCUSSION AND CONCLUSIONS
- - When relativistic equations are applied to the rectilinear experiments
of Figs. 3, 4, 6, and 12 the predicted induced (Lorentz) field, v x
B, is always 0. This is true both for an observer fixed to the moving
magnet M and for one fixed to the Lab. (See detailed equations in
Ref. 3). Yet, in Figs. 6 and 12 the experiments show a positively induced
v
x B effect. Relativity theory, being a local field theory, cannot take
into account the crucial role played by the distant transversal edges of
the magnets, which are present in Figs. 3 and 4, (Killing" the induction),
and absent in Figs. 6 and 12, allowing it to happen. Hence, Special Relativity
FAILS in an experiment (Fig. 12) which is at the heart of its domain of
application, (the electrodvnamics of moving bodies). And the General Theory
cannot come to the "rescue" (no accelerations are involved).
WE NEED, THEREFORE, A NEW PHYSICS FOR THE 21st CENTURY!
REFERENCES
(1)
- Panofsky, W. & Phillips, M., Classical Electricity and Magenetism,
Addison-Wesley, Reading, MA., Sect. 18-6, (1962).
(2)
- Schiff, L.I., "A Question in General Relativity", Proc. Nat. Acad.
Sci, Vol. 25, p. 391, (1939).
(3)
- Müller, F.J., "Unipolar Induction", Galilean Electrodynamics,
Vol. 1, p. 27, (1990).
COMMENTS?
Write to: F. J. Müller
8025 SW 15 St.
Miami, Florida 33144 USA
varelaacademy@iscnet.net
